GET3D
英伟达
Motivation
-
目前3D模型生成需求非常大(比如游戏建模,还有元宇宙)。最传统的方式是建模师去人工建模,但是这样的方式非常耗时耗力,人工在短时间内生成大量3D模型不太现实。依据当前的需求,3D模型生成的模型,希望能够满足如下条件:
- 能生成详细的集合细节与拓扑形状;
- 能够输出纹理网络(显式表达),以能够输入到现有软件中进行编辑和应用;
- 在训练时使用2D图像进行监督(因为比3D的图像能容易获得)。
-
目前的生成模型都不能同时满足以上的需求:
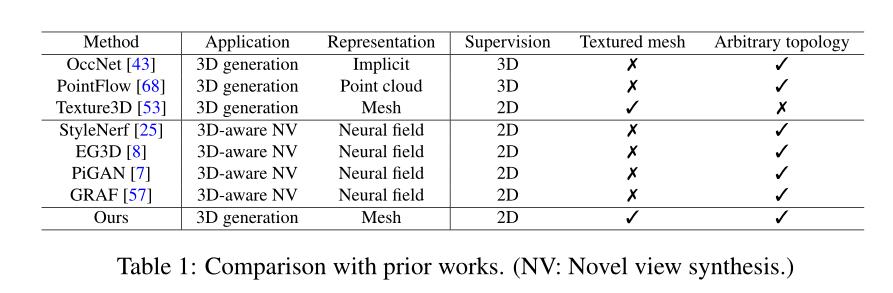
Contribution
- 提出了GET3D模型,该模型满足所有提出的条件:能够直接生成显式的3D纹理网络,并且能够控制纹理细节与拓扑结构;该模型结合了可微显式表面提取与可微渲染,前者能够直接优化和输出具有任意拓扑的3D纹理网格,后者能够用2D图像训练模型,能够使用现有2D图像合成任务中比较成熟的鉴别器。
- 可以拓展到其他任务:使用CLIP嵌入的文本指导形状生成;在无监督的条件下,学习使用先进的可微渲染技术生成分离出来的材料(decomposed material,材料纹理图片?)和依赖于视图的照明效果。
Method
- GET3D整体模型架构与训练/推理流程:
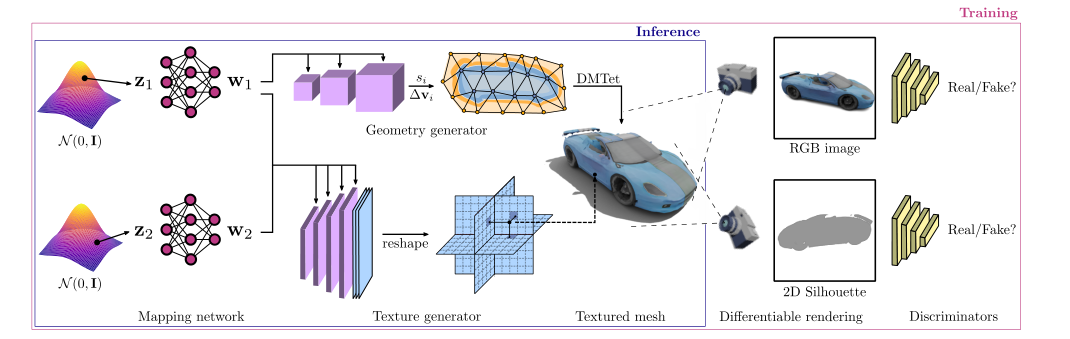
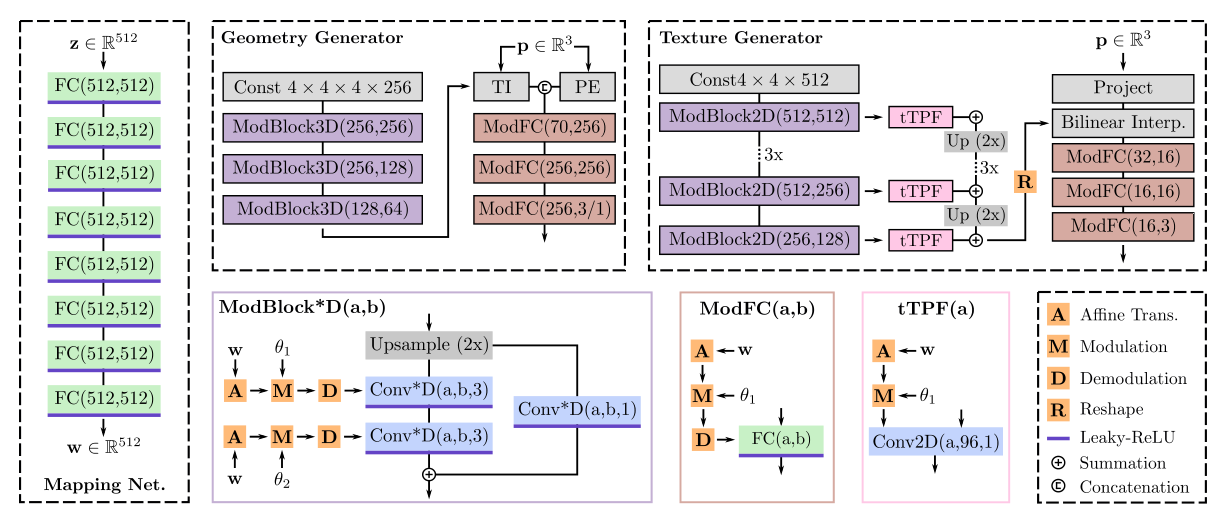
Mapping Network
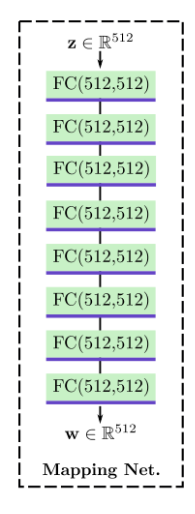
- 由于相同形状的物体可以有不同的材质、相同的材质又可以运用到不同形状的物体上,因此可以视为二者相互独立,因此要单独控制。
- 随机选取 和,依照StyleGAN的方式通过两个非线性映射与,得到两个隐变量 和,它们会分别控制几何形状与材质。
- Mapping network是一个8层的全连接网络,维度为512,每层激活函数为 leaky-ReLU,整体与StyleGAN相同。
Geometry Generator
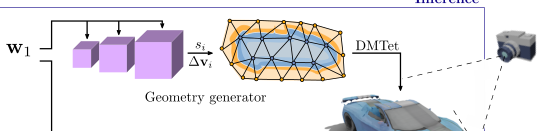
- 几何生成器(Geometry generator)的目标是将结果可以应用到DMTet(一个最近提出的可微的表面表示方法)中。
- 设表示四面体网络T的顶点的集合,用可以表示整个物体所在的四面体空间;网络中的每个由四个顶点定义。,是四面体的总数。每个顶点记录了三维坐标、SDF的值、形变量。
- 这种表示方法可以通过可微行进四面体(Differentiable Marching Tetrahedra)恢复显式网格(Mesh);变形顶点上的SDF值通过重心插值计算得到连续空间中的SDF值。
- 在需要高分辨率建模的情况下(如车轮的纹理),进一步使用DMTet中的体积细分法。
Network Architecture
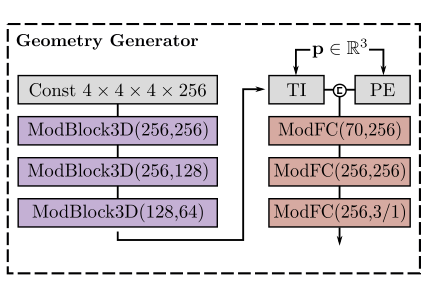
-
网络由一系列的三维卷积与全连接层组成,将采样的得到的映射到SDF的值与顶点的形变量。使用条件三维卷积层来生成一个以为条件的特征;然后使用三线性插值查询每个顶点的特征,并将其输入到MLP,得到SDF值和变形量。
-
随机初始化一个特征量,它的权重在所有输入中共享,是一个可学习的参数;经过三个ModBlock3D(Modulated 3D Convolution Block):
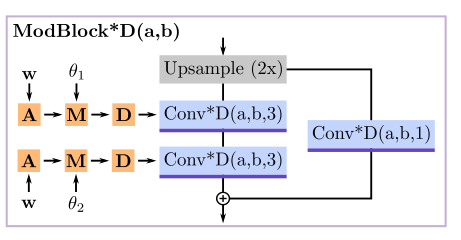
图为ModBlock*D,*代表不同维度但结构相同,比如纹理生成的部分还使用到了ModBlock2D。
-
在每个ModBlock3D中首先使用双线性插值的方式对特征进行上采样,接着经过一个3D-ResNet,残差路径使用卷积核大小为,主路径为。
-
对于条件,首先进行仿射变换到,被用于调制(M)和解调(D)条件卷积层的权重:
其中,和分别是初始与调制后的权重,是第个输入通道的style(StyleGAN中的说法),为输出通道维数,为三维卷积滤波器的空间维数。
-
经过卷积之后即可得到特征,再对其进行三线性插值(TI),得到每个顶点的特征向量,再对该向量对应顶点的坐标进行位置编码(PE),将向量与位置编码后的位置进行拼接输入到ModFC中。
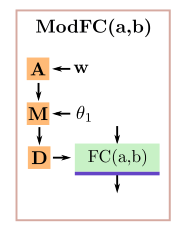
ModFC包括一个全连接层,与ModBlock类似经过了调制与解调的过程。拼接后的结果经过三层的ModFC,中间使用leaky-ReLU作为激活;最后一层使用tanh,将SDF的值归一化到,将形变归一化到,tet-res表示四面体网络的分辨率(原实验设置为90)。
Differentiable Mesh Extraction
-
在获得所有顶点的SDF和形变量的值后,使用可微行进四面体算法(Differentiable Marching Tetrahedra Algorithm)提取显式网格。
-
行进四面体根据的符号确定每个四面体的拓扑结构,当时即可以确定一个表面,其中i, j表示四面体边缘的顶点索引,然后该面的顶点通过线性插值的方式确定:
-
当且仅当时才会进行计算(分母非0),因此是可微的,即可通过反向传播优化。
-
通过预测的不同符号即可生成任意拓扑形状。
Texture Generator
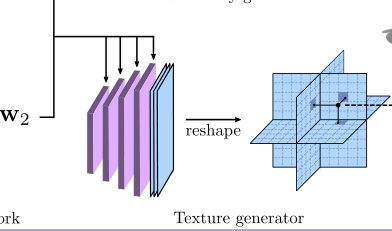
-
纹理生成将纹理参数化为一个纹理场(Texture field);纹理场用三平面表示(更高效)。
-
具体来说,用函数对纹理场进行建模,将三维的点,以(由于纹理与几何有关)与为条件映射到该位置的RGB颜色值。因此:
-
与传统工作光线追踪不同的是,本工作获得颜色的方式是直接输入图像表面的三维坐标即可查询到对应的颜色,极大简化了渲染的复杂度并且保证了多视图的一致性。
Network Architecture
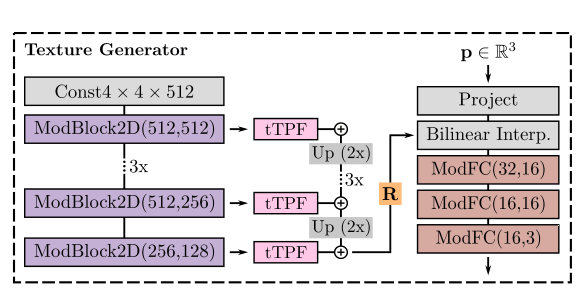
- 与StyleGAN2类似的网络结构,使用条件二维卷积网络将映射成大小为的三平面坐标。(N=256,C=32)
- 随机初始化一个特征网络$ F_{tex} \in \mathbb{R_{4 \times 4 \times 512}}\mathbf{w_{1}} \oplus \mathbf{w_{2}}$,维度为2)。
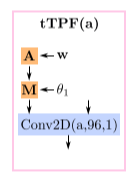
- 每一层ModBlock2D的输出分别经过一个tTPF网络,tTPF为一个卷积核为的条件卷积网络,根据StyleGAN2,tTPF只进行调制(M)而不进行解调(D),首先将条件进行仿射变换,与几何生成(Geometry Generator)部分介绍的方法相同,计算条件卷积的初始权重。最后特征网络被上采样到。
- 给定一个特征表面上的点,计算特征向量,其中表示向e平面投影,表示双线性插值,然后通过三层全连接层将特征向量和位置转化为颜色。
Differentiable Rendering
- 假设数据集中相机的分布为,随机采样一个相机c,使用Nvdiffrast将重建的3D网络转化为2D图像与轮廓,每个像素包含了3D图像的坐标;这些坐标进一步用于查询纹理场进而获得RGB颜色值。
- 由于直接在生成的Mesh上操作,因此可以高效率地渲染高分辨率图像,允许模型训练图像分辨率高达1024×1024。
Discriminator
-
与StyleGAN的鉴别器架构相同,使用两个鉴别器来训练GET3D:一个用于RGB输出,一个用于2D轮廓。
-
使用与StyleGAN相同的带有R1正则化的非饱和GAN目标(Non-saturating GAN Objective)。令表示判别器,其中可以是RGB图像或2D轮廓,则对抗优化目标定义如下:
其中,是图像的分布。
-
为了去除在任何视图中都不可见的内部浮动面(internal floating faces),用相邻顶点的SDF值的交叉损失熵来进一步规范几何生成:
- 最终的损失函数:
