GRAF

University of Tübingen

Motivation

• 传统的图像生成通常基于GAN网络，已经可以生成清晰足以以假乱真的图片，但是以这种方式学习得到的模型忽视了生成因素（与人类理解或绘制一张图的方式相比），比如光线与物体的关系等等（文章中表述为潜在因素）。
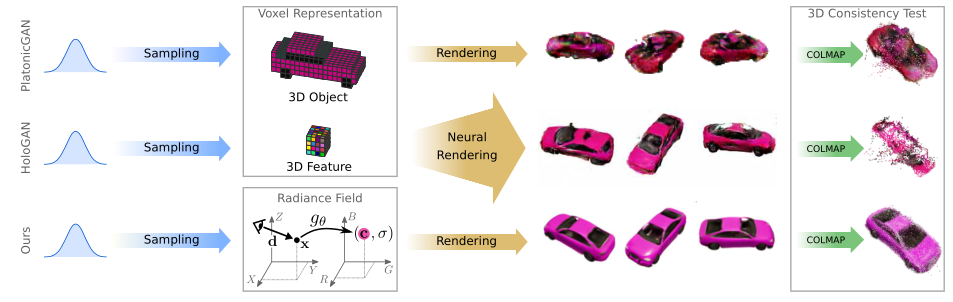
• 近期有工作提出了3D感知图像生成，在生成图像时考虑了相机的姿态，使用可微渲染技术显式映射到图像，从而提供对场景内容和视点的控制。但是真实的3D图像难以得到，因此一般采用2D的图像进行监督，获得2D图像的方式一般需要：离散化3D表示，比如中间特征（HoloGAN）或者完整的3D特征（PlatonicGAN）的体素网络。若采用完整的体素网络表示，体素的表示的三次内存增长将限制为低分辨率并导致可见伪影；相反虽然中间特征的体素网络更紧凑，但是这需要额外学习 3D 到 2D 的映射，以将抽象特征解码为 RGB 值，从而导致在高分辨率视图中表示的不一致性。

Contribution

• 本文证明了分辨率低（内存限制）、高分辨率的不一致性（中间表示的不足）可以用条件辐射场来解决。
• 具体的贡献：
  1. 提出了GRAF——基于未处理的图像，进行高分辨率的3D感知图像合成的辐射场的生成式模型（GAN）。除了改变视角，该模型还允许修改物体的形状和外观。
  2. 引入了一个基于补丁的判别器，它在多个尺度上对图像进行采样，是学习高分辨率生成性辐射场的关键。

Method

NeRF

• 首先介绍了NeRF的原理（本文方法的基石），很多文章都介绍过了，所以略过此部分。

Generative Radiance Fields

• 与NeRF的方式不同，GAN的方式不需要假设有大量的带有姿态信息的图像，而是通过“unposed images”来进行训练，并且能够生成新的场景。
• 整个流程如下：

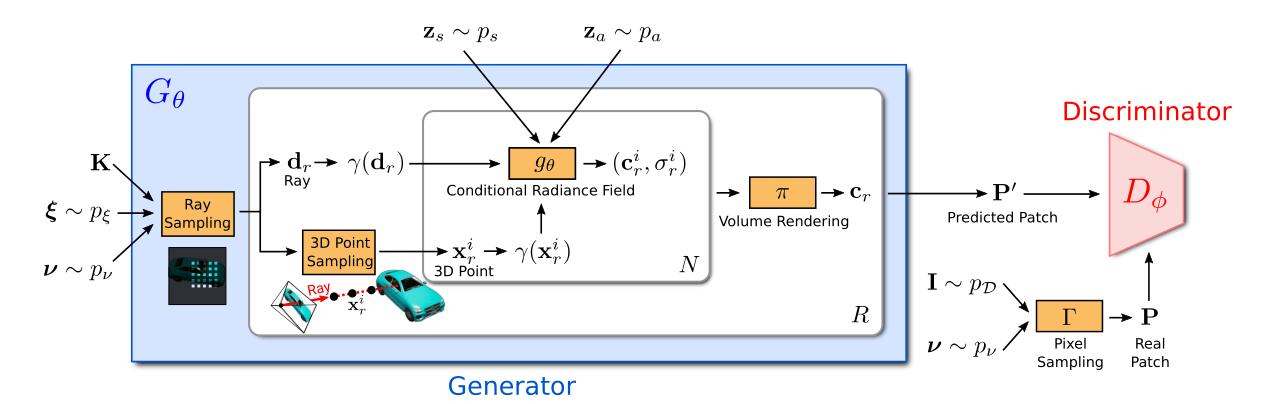
符号定义

• 涉及的符号有点多….

  • $G_{\theta}$表示整个生成网络；$D_{\phi }$表示鉴别器。

  • $\textbf{K}$表示相机矩阵，它使得相机畸变中心（principle point）始终位于图像的中间。

  • $\xi = [\textbf{R}|\textbf{t}]$表示从分布为$p_{\xi}$分布采样得到的相机的姿态。这个分布是一个空间坐标系上半部的均匀分布，相机朝向为坐标原点。

  • 假设采样的图像补丁$\mathcal{P}(\mathbf{u}, s)$（patch）大小为$K \times K$。$\nu =(\textbf{u},s)$代表二维（即图像平面）的采样方式，具体来说，$\textbf{u}=(u,v)$表示采样中心的坐标，$s$代表了图像补丁的尺度。其中，u服从整个图像域上的均匀分布$\mathbf{u} \sim \mathcal{U}(\Omega)$，尺度s服从$s \sim \mathcal{U}([1, S])$的均匀分布，$S=min(W,H)/K$。

    

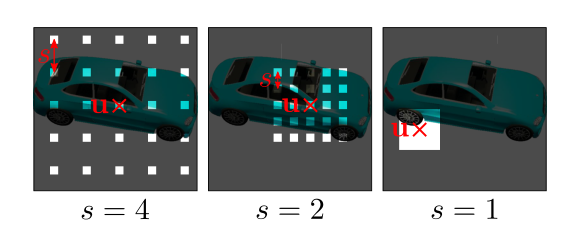
  • $z_{s}\sim p_{s}$与$z_{a} \sim p_{a}$分别表示形状与外观的“码”（code），二者都服从标准的高斯分布（即均值为0 方差为1的正态分布）。

  • $\gamma(\mathbf{x})$与$\gamma(\mathbf{d})$分别表示位置编码与方向编码（与NeRF相同）。

  • 图像I的真实分布记为$p_{D}$。

Generator

Ray Sampling

• 具体而言，图像补丁$\mathcal{P}(\mathbf{u}, s)$如下定义：

  $$\mathcal{P}(\mathbf{u}, s)= \{\ (s x+u, s y+v) \mid x, y \in \{\ -\frac{K}{2}, \ldots, \frac{K}{2}-1 \}\ \}\$$

  它描述了像素的位置。由上式可以看出，$\mathcal{P}$即是与s和u有关的坐标，前者是缩放，后者为中心偏移。注意的是x与y都是连续的量，这样可以连续地评估辐射场。

• 每一条光线都由$\mathcal{P}$、相机姿态$\xi$、和矩阵K决定。

• 用r表示像素/射线，用$\textbf{d}_{r}$表示归一化之后的射线，R表示射线的数量，其中训练时$R=K^{2}$（减少开销与提升速度），推理时$R=HW$。

3D Point Sampling

• 与NeRF的做法一致，都是采用分层抽样的方式。

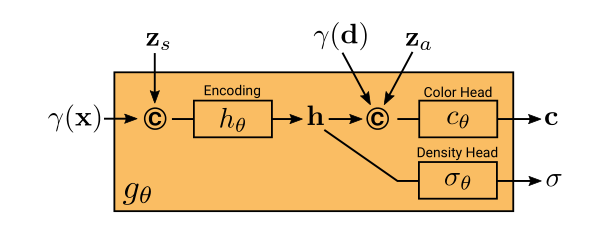
Conditional Radiance Field

• 条件辐射场：

• 与NeRF的辐射场（输入为体密度和颜色）不同，本文提出的方法还需要颜色码和外观码控制，所以叫做条件辐射场（好牵强- -b）。

• 这一部分是唯一需要学习的，流程大致为：

  • 首先位置编码与形状码一起输入计算得到形状编码h，网络内有一个被称为密度头$\sigma_{\theta}$（density head）的部分，将h转换为体密度$\sigma$。
  • h和方向编码、外观码一起，通过一个被称为颜色头$c_{\theta}$（color head）的部分，被转化为颜色c。
  • 这些部分都是由全连接网络实现的，使用ReLU作为激活函数。

• 从整个流程来看：

  • 首先，体密度也就是形状的预测与颜色无关（从直观上来讲，形状本身也与颜色无关）。体密度的预测独立于颜色（外观），以期能够保证多视图的一致性。
  • 其次，对于颜色的预测，它不仅依赖于视角d与颜色码，还依赖于形状（从直观上讲，首先一个物体不同位置的颜色可能不一样，其次由于光线影响，不同视角的观察到的颜色也有区别），以此建模为视角依赖的外观（比如镜面反射）。
  • 这种方式可以使得外观码与形状码能够分别独立地控制形状与外观。

• 将其数学化表示，即：

  $$h_{\theta}: \mathbb{R}^{L_{\mathbf{x}}} \times \mathbb{R}^{M_{s}} \rightarrow \mathbb{R}^{H} \qquad \qquad(\gamma(\mathbf{x}), \mathbf{z}_{s}) \mapsto \mathbf{h}$$

$$c_{\theta}: \mathbb{R}^{H} \times \mathbb{R}^{L_{\mathbf{d}}} \times \mathbb{R}^{M_{a}} \rightarrow \mathbb{R}^{3} \qquad \qquad (\mathbf{h}(\mathbf{x}, \mathbf{z}_{s}), \gamma(\mathbf{d}),\mathbf{z_a}) \mapsto \mathbf{c}$$

$$\sigma_{\theta}: \mathbb{R}^{H} \rightarrow \mathbb{R}^{+} \qquad \qquad \qquad \qquad \mathbf{h}(\mathbf{x}, \mathbf{z}_{s}) \mapsto \sigma$$

Volume Rendering

• 使用与NeRF相同的体渲染方式，对每一条射线上的采样点进行计算，得到颜色值，将所有的预测位置结合之后，得到了预测的图像补丁（这个补丁所处位置的颜色）。

Discriminator

• 鉴别器首先要获得真实图像分布下的补丁（patch），与生成器的操作相同，根据$\nu =(\textbf{u},s)$确定采样的位置与缩放，然后使用双线性插值的方式获得对应处的真实补丁$\textbf{P}$。为了与生成器做区分，使用$\Gamma=(\textbf{u},s)$表示鉴别器的双线性插值采样方式。
• 鉴别器的思路来源于PatchGAN，与其不同的是，本文的方法是连续的坐标以及多种s（PatchGAN将s固定为1）。从采样示例图可以看出，采样的过程不会基于s对真实图像$\textbf{I}$进行下采样，而是在稀疏位置采样$\textbf{I}$以保留高频的信息。
• 鉴别器是一个卷积神经网络，而且只使用一个共享权重的鉴别器即可适用于不同图像补丁。
• 缩放比例s决定了补丁的感受野。为了促进训练，先从较大的感受野的补丁开始以捕获全局上下文相关信息。接着逐步对具有较小感受野的补丁进行采样，以优化局部细节。

Train

• 使用具有R1正则化的非饱和GAN目标来训练：

  $$\mathbb{E_{\mathbf{z_{s}} \sim p_{s}, \mathbf{z_{a}} \sim p_{a}, \xi \sim p_{\xi}, \nu \sim p_{\nu} }}[f(D_{\phi}(G_{\theta}(\mathbf{z_{s}}, \mathbf{z_{a}},{\xi}, {\nu})))] \\ +\mathbb{E_{\mathbf{I} \sim p_{D}, \boldsymbol{\nu} \sim p_{\nu}}}[f(-D_{\phi}(\Gamma(\mathbf{I}, \boldsymbol{\nu})))-\lambda\|\nabla D_{\phi}(\Gamma(\mathbf{I}, \boldsymbol{\nu}))\|^{2}]$$

其中$f(t)=-\log (1+\exp (-t))$， $\lambda$表示正则化的强度。并且在判别器中使用光谱归一化（spectral normalization）和实例归一化（instance normalization）。