A review of Denoising Diffusion Probabilistic Models

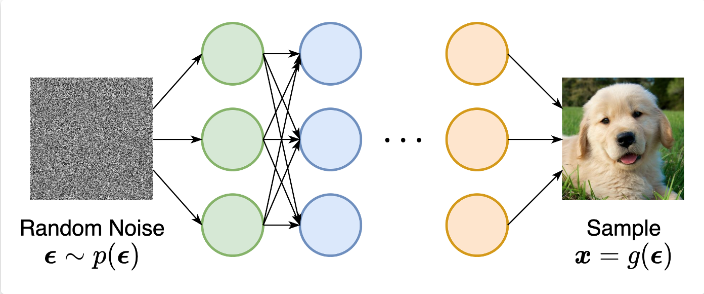
Introduction

​ 现在 (2023年3月29日) 所谓的扩散模型大多数指的是2020年所发表的Denoising Diffusion Probabilistic Models，简称为DDPM。其实“扩散”的思想更早见于Diffusion Probabilistic Models(Sohl-Dickstein et al.)，但是由于当时的算力以及模型计算Loss是基于图像而不是噪声，所以没有很好的效果。

​ 在2020年以后，许多基于原始DDPM模型的工作开始大量出现，包括对模型的架构、采样过程、图像预处理的改进，当然扩散的思想也不再局限于计算机视觉(CV)领域，而是开始应用于多模态(Multimodal)、自然语言处理(NLP)、语音(Audio)等各种领域。而在2022年，OPENAI的DALL·E 2以及后来的NovalAI的成功，让扩散模型商用化（当然训练模型所用的资源也是我们无法想象的😱）,也让“扩散模型”进入了大众的视野（比如我😁）。

​ 作为一种生成式模型，DDPM的出现打破了GAN、VAE等在图像生成领域的“垄断”，它有着很强(?)的数学理论，解决了生成前辈们的存在的一些问题，当然DDPM也借鉴了一些前述工作的成果。鉴于DDPM的成功，本文所说的扩散模型指的是DDPM以及基于其的改进模型。

Background

​ 在介绍DDPM之前，首先要整理一下其所涉及的一些数学背景，以免在后面推导时不知所云。可以直接跳到下一部分🦁。

Markov Chain

马尔科夫链/过程

​ 学过随机过程的话应该对Markov十分熟悉了，这里只讨论与扩散模型相关的有限状态的离散时间时齐的马尔可夫链。假设一个状态链，其下一个过程只与当前的状态有关，而与其他的更久远的状态无关。

​ 我们观测一个随机状态的变化，其序列为$\{x_0,x_1,...,x_t,...,x_T\}$，转移概率根据条件概率应该为$p(x_{t+1}|x_t,x_{t-1},...,x_0)$，再根据马尔可夫链的性质，简化为$p(x_{t+1}|x_t)$。如果要求其反转的过程，可以根据贝叶斯定理：

$$p(x_{t}|x_{t+1})=\frac{p(x_{t})p(x_{t+1}\mid x_{t})}{p(x_{t+1})}$$

Gaussian Distribution

高斯分布与其相关性质

​ 高斯分布又称为正态分布，对于一个连续时间的高斯分布，若随机变量$X$服从均值为$\mu$，方差为$\sigma$的高斯分布，简记为$X\sim N(\mu,\sigma^2)$或者$X\sim N(x;\mu,\sigma^2)$，当均值为1，方差为0时，我们称它为标准高斯（正态）分布。其概率密度函数可以写为：

$$f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}$$

​ 高斯分布有很多性质，常见的有：

• 假设有实数$a$、$b$，则对于$X\sim N(\mu,\sigma^2)$有$a X+b\sim N(a\mu+b,(a\sigma)^2)$。
• 假设$X$与$Y$独立，且$X\sim N(\mu_{X},\sigma_{X}^{2})$、$Y\sim N(\mu_{Y},\sigma_{Y}^{2})$，则$X+Y\sim N(\mu_{X}+\mu_{Y},\sigma_{X}^{2}+\sigma_{Y}^{2})$也服从高斯分布。

Reparameterization

重参数化技术

​ 假设有一系列样本$x$，我们想求得某一分布$p_{\theta}(x)$。如果通过深度学习的方式去学习，一般要求最小化：

$$L(\theta,\phi)=\mathbf{E}_{x\sim\rho_\phi(x)}[f_\theta(x)]$$

​ 我们要对其进行梯度计算以进行反向传播，$L$是关于$\theta,\phi$的函数，也即$\nabla_\theta L(\theta,\phi)$以及$\nabla_\phi L(\theta,\phi)$。

• 对于$\nabla_\theta L(\theta,\phi)$，根据Leibniz法则有：

  $$\nabla_{\theta}\mathsf{L}(\theta,\phi)=\nabla_\theta\mathbf{E}_{x\sim p_{\phi}(x)}\left[f_{\theta}(x)\right]=\mathbf{E}_{x\sim\mathcal{p}_{\phi}(x)}\left[\nabla_θ f_{\theta}(x)\right]$$

  然后可以根据Monte-Carlo方法求出：

  $$\nabla_{\theta}L(\theta,\phi)\approx\dfrac{1}{|S|}\sum\limits_{s=1}^S\nabla_\theta f_\theta\left(x^{(s)}\right)$$

​ 其中$x^{(s)}$从${p}_{\theta}(x)$中采样，$f$是关于$\theta$可导的。

• 对于$\nabla_\phi L(\theta,\phi)$，同样由Leibniz法则有：

  $$\nabla_\phi L(\theta,\phi)=\nabla_{\phi}\mathbf{E}_{x\sim\boldsymbol{p}_{\phi}(x)}\left[f_{\theta}(x)\right]=\int f_\theta(x)\nabla_\phi p_\phi(x)dx$$

  此时Monte-Carlo方法并不能起作用，因为Monte-Carlo只能通过采样得到值，而不能告诉我们它的梯度是多少，简单来说就是“采样”这个过程不可微。

​ 而重参数化就是把随机性从变量中“分离”出来，设一个确定性函数$x=g(\phi,\epsilon)$，$\epsilon$表示一个随机变量，此时求导时就会绕过$\epsilon$这个随机的项。对于$\nabla_\phi L(\theta,\phi)$就变为：

$$\nabla_{\phi}L(\theta,\phi)=\mathbf{E}_{\epsilon\sim p(\epsilon)}\left[f'_{\theta}(g(\phi,\epsilon))\nabla_{\phi} g(\phi,\epsilon)\right]$$

​ 因此，对于一个密度函数，要如何求得这个确定性函数😶？对于常见的数据分布，已经有很完备的推导了：

​ 对于扩散模型，我们要用到是简单的高斯分布的重参数化，可以写为：

$$x=\mu(\phi)+\sigma(\phi)*\epsilon$$

​ 其中，$\epsilon\sim N(0,1)$。

Stochastic Differential Equation

随机微分方程

​ 对于一个随机过程（比如布朗运动），我们能否用一个方程来表述呢（类似于一辆车行驶在公路上，我们可以用牛顿定律去描述）？随机届的Stochastic Differential Equation（简称为SDE）就是用来描述随机过程的工具。一般来说，对于概率上的SDE的一个典型的形式为：

$$\mathrm{d} X_{t}=\mu\left(X_{t}, t\right) \mathrm{d} t+\sigma\left(X_{t}, t\right) \mathrm{d} B_{t}$$

​ $B$代表标准布朗运动（维纳过程）。它的积分形式为：

$$X_{t+s}-X_t=\int_{t}^{t+s}\mu(X_u,u)\mathrm{d}u+\int_t^{t+s}\sigma(X_{u},u)\mathrm{d}B_{u}$$

​ 上述方程将连续时间的$X_t$描述为勒贝格积分（Lebesgue integral）与伊藤微积分（Itō calculus）之和，上过数学分析的应该对勒贝格积分有一些印象，伊藤微积分将微积分的概念扩展到随机过程中，分别详见勒贝格积分 与伊藤积分。对于这个积分项，我们很直观的看出，对于一个$s$小间隔的$X_t$的变化，服从均值为$\mu(X_t,t)$方差为$\sigma(X_{t},t)^2$的正态分布，并且与过去的状态无关（只与$t$时刻有关）。我们称$\mu$称为漂移系数（drift coefficient），而$\sigma$称为扩散系数（diffusion coefficient），随机过程$X_t$称为扩散过程，满足马尔可夫相关的性质。

​ 通过这样的一个过程，我们把$x_0$到$x_T$建立起了联系，但是有没有一种随机微分方程可以从$T$到0，按照规矩我们可以称它为逆时间随机微分方程（Reverse-time SDE），结论是可以，但是推导比较复杂🤯，详见这个Blog，最后结果为：

$$\mathrm{d} X_{\tau}=\Big(-\mu(x_{1-\tau})+\tilde{\sigma}^2\partial_{x_{1-\tau}}\log p(x_{1−\tau})\Big)dt+\sigma(x_{1-\tau})d\tilde{W}_\tau$$

Evidence Lower Bound（ELBO）

证据下界

​ ELBO可见于期望最大化和变分推理，尤其是了解过VAE模型的人。

​ 假设存在一个隐变量$z$，它反映着分布的结构等等（比如Encoder-Decoder架构的中间变量），我们在建模的时候通常得到$p(x,z;\theta)$，$\theta$是网络超参数（后续省略），我们可以通过对变量$z$进行积分$p(x)=\int p(x, z)dz$，或者链式法则：

$$p(x)=\dfrac{p(x,z)}{p(z|x)}$$

​ 从联合分布$p(x,z)$得到我们真正需要的$p(x)$：积分的方式需要我们去遍历所有的$z$，链式法则的方式需要我们知道真实分布是怎么样的（都知道了还建啥模🤣）。

​ 因此我们要换个方向去解决，用模型$q_{\phi}(z \mid x)$去拟合$p(z|x)$。首先我们根据最大似然的常用手段，去最大化对数似然$\log(p(x))$，我们对其进行一个简单的推导（推导涉及条件概率计算与概率密度的积分，应该不难😉）：

$$\begin{aligned} \log p(\boldsymbol{x}) & =\log p(\boldsymbol{x}) \int q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x}) d z \\ & =\int q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})(\log p(\boldsymbol{x})) d z \\ & =\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}[\log p(\boldsymbol{x})] \\ & =\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{p(\boldsymbol{z} \mid \boldsymbol{x})}\right] \\ & =\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z}) q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}{p(\boldsymbol{z} \mid \boldsymbol{x}) q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\right] \\ & =\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\right]+\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}{p(\boldsymbol{z} \mid \boldsymbol{x})}\right] \\ & =\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\right]+D_{\mathrm{KL}}\left(q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x}) \| p(\boldsymbol{z} \mid \boldsymbol{x})\right) \\ & \geq \mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\right] \end{aligned}$$

​ 因为KL散度（Kullback–Leibler Divergence，或者叫相对熵）是非负的，所以能得到最后一步。此时，我们称$\log p(\boldsymbol{x})$为证据，则$\mathbb{E}_{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\left[\log \frac{p(\boldsymbol{x}, \boldsymbol{z})}{q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x})}\right]$就为ELBO。

$\log p(\boldsymbol{x})$被称为证据的原因是如果我们选择了正确模型$p$和参数$\theta$，那我们就会有很大的概率输出正确的数据，$\log p(\boldsymbol{x})$也就会很大，因此$\log p(\boldsymbol{x})$是我们为数据选择正确模型的 “证据”。

​ 为什么去最大化ELBO能优化$\log p(\boldsymbol{x})$呢🤔。首先$\log p(\boldsymbol{x})$是与$\phi$无关的，因此，我们在最优化参数$\phi$时，我们的证据大小是不变的，当ELBO增加时，为了保证证据大小不变，$D_{\mathrm{KL}}\left(q_{\phi}(\boldsymbol{z} \mid \boldsymbol{x}) \| p(\boldsymbol{z} \mid \boldsymbol{x})\right)$一定会减小，换句话说就是$q_{\phi}$与$p_{\theta}$更像了。然后我们就能得到数据的近似分布$p(x)$。

更详细与广泛的说明见这个Post。

Related Work

Overlook

​ 既然DDPM是一种生成式的模型，那么就有必要对生成式模型这个大家族进行一些介绍。对于其他生成式模型，我也不能说十分了解，也是看了一些皮毛，有错误欢迎指出与讨论🤗🤗

​ 生成式模型（Generative Models），顾名思义就是一种用于生成的模型，与之相对的比如判别式的模型，说得数学一些就是判别式的模型去直接学习一个条件概率密度分布，如果用$X$代表源域，$Y$代表目标域，那么判别式的模型就去学习直接拟合$P(Y|X)$函数，而生成模型去学习联合分布$P(X,Y)$。

因此生成模型能够用于模拟（即生成）模型中任意变量的分布情况，而判别模型只能根据观测变量得到目标变量的采样。判别模型不对观测变量的分布建模，因此它不能够表达观测变量与目标变量之间更复杂的关系。因此，生成模型更适用于无监督的任务，如分类和聚类。

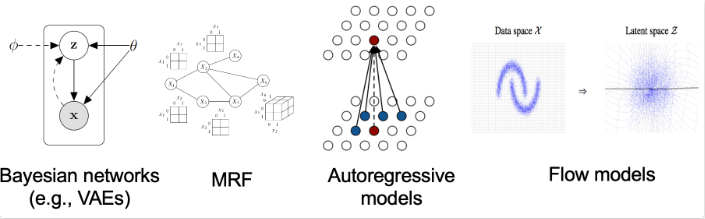
​ 常见的生成式模型包括自回归模型、归一化流模型（Normalizing Flow）、基于能量的模型（EBMs）、变异自动编码器（VAEs）、以及对抗生成网络（GANs）和现在的去噪扩散概率模型（DDPM）。

在以前，这些模型根据根据其表示概率分布的方式可以大致分为两类：

1. 基于似然的模型（Likelihood-based Models），它通过（近似的）最大似然直接学习分布的概率密度函数。典型的基于似然的模型包括自回归模型、归一化流模型、基于能量的模型和变异自动编码器，所有这些模型都表示一个分布的概率密度或质量函数。

   

2. 隐式生成模型（Implicit Generative Models），其概率分布由采样过程的模型隐含表示。比如生成对抗网络（GANs），其数据分布的新样本是通过用神经网络转换随机高斯向量而合成的。

   

   图都来自于宋飏博士的Blog

​ 上述两种模型都存在一定的问题，比如基于似然的模型需要确保能够得到一个归一化常数（用来确保概率之和为1的常数），如果无法计算归一化常数，则需要使用近似方法来进行最大似然训练。而GANs要训练生成器与判别器，在训练的过程需要对抗性训练，非常不稳定，可能导致模式崩溃（Mode Collapse）。

​ 对于归一化常数，举个🌰，对于一个连续的概率密度函数，我们对其进行积分，肯定要保证其积分为1，比如我们耳熟能详的高斯分布：$f(x) = \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)2}{2\sigma^2}}$，归一化常数其实就是$\frac{1}{\sqrt{2\pi}\sigma}$，用于确保概率密度函数在整个定义域上的积分为1。但是在训练模型的时候概率分布肯定不是这么简单的，因此有时计算归一化常数并不是很简单的🤯

为了使模型能够进行最大似然训练，我们需要对模型结构进行限制或使用近似方法，避免归一化常数的计算。

Score-based Models

​ 为了解决上述两种模型存在的问题，一种基于分数的模型（Score-based Models）横空出世。

其关键思想是对对数概率密度函数的梯度进行建模，通常被称为（Stein）分数函数（Score Function）。这种基于分数的模型不需要有一个可计算的归一化常数，可以通过分数匹配（Score Matching）直接学习。

​ 基于分数的模型与DDPM有很大的关系，因此要对分数模型进行介绍🤗（事实上，基于分数的模型和DDPM是同一事物的两种不同的解释，非常推荐宋飏大佬的这篇Blog：Generative Modeling by Estimating Gradients of the Data Distribution！🥳这一部分大部分都是基于这个Blog😁）

​ 给定一些独立同分布的数据，即从$p(x)$中采样得到$\{x_1,x_2,x_3,...,x_t\}$，生成模型就是去得到这个$p(x)$，比如前面提到的似然方法就是去直接得到这个$p(x)$。根据似然模型，假设这个分布的密度函数为：

$$p_{\theta}(x)=\frac{e^{-f_{\theta}(x)}}{Z_{\theta}}$$

​ 其中，$-f_{\theta}(x) \in \mathbb{R}$称为非标准化概率模型（Unnormalized Probabilistic Model），或基于能量的模型（Energy-based Model），$Z_{\theta} > 0$就是前面提到的归一化常数，$\theta$就是可学习的参数。如果想训练这个模型就最大化似然即可：

$$\max_{\theta } \sum_{i=1}^{N}\log p_{\theta}(x_i)$$

​ 至此，好像没啥特别的，我们还要去和最大似然模型一样去做这些很困难的任务🤔，比如像自回归模型的因果卷积、归一化流模型中的可逆网络，抑或是去估计归一化常数，比如VAE中的变分推理等等。

​ 但是，换个角度，既然我们定义了$f_{\theta}(x)$，那么是不是可以想个办法绕过直接对密度函数建模？还真行🥳——定义一个称为得分函数（Score Function）的东西，对于$p(x)$，它的得分函数被定义为：

$$\nabla_{x}\log p(x)$$

​ 我们将基于得分函数的模型，就叫做基于分数的模型（Score-based Model），假设模型为$s_{\theta}$，我们的目标就是尽量让$s_{\theta}$与$\nabla_{x}\log p(x)$相等，这样我们就绕过了归一化常数。那和能量模型$f_{\theta}(x)$有啥关系？将其展开：

$$\mathbf{s}_{\theta}(\mathbf{x})=\nabla_{\mathbf{x}}\log p_\theta(\mathbf{x})=-\nabla_\mathbf{x}f_\theta({\mathbf{x}})-\underbrace{\nabla_\mathbf x\log{Z}_\theta}_{=0}=-\nabla_\textbf x f_\theta(\mathbf x)$$

​ 这样我们成功绕过了归一化常数（数学上）🎉，而且由于没有归一化常数的限制，我们可以随意扩展与修改模型。（在宋博的Blog上有可视化更直观😁）

​ 通过最小化模型和数据分布之间的Fisher散度（Fisher Divergence）来训练基于分数的模型（衡量真实数据与基于分数的模型之间的$l_2$的平方的距离），定义为：

$$\mathbb{E}_{p(\mathbf{x})}[\|\nabla_\mathbf{x}\log p(\mathbf{x})-\mathbf{s}_\theta(\mathbf{x})\|_2^2]$$

​ 我们没法直接计算$\nabla_\mathbf{x}\log p(\mathbf{x})$，但是，有一种方法可以解决这个问题——分数匹配（Score Matching），能够在真实数据分布未知的情况下去最小化Fisher散度。它能直接在数据集上进行估计并进行优化（不需要考虑归一化常数，也不需要与GAN一样的对抗）。

​ 综上所述，通过对分数函数进行建模，我们绕过了归一化常数的问题，并且有一个完备的优化它的方式。但是我们的建模是$\nabla_{x}\log p(x)$而不是$p(x)$，我们还需要解决采样从而得到我们想要的数据🤨。这个方式就叫做朗之万动力学（Langevin Dynamics）。

Langevin Dynamics

​ 与SGDM的灵感来源类似，分数模型的采样过程也来源于物理学，即朗之万动力学，它允许我们从一个任意的分布，只根据$\nabla_\mathbf{x}\log p(\mathbf{x})$迭代计算“采样”，假设初始分布为$x_{0}$：

$$x_{i+1}\leftarrow x_i+\epsilon\nabla_x\log p(x)+\sqrt{2\epsilon}\mathbf{z}_i,\quad i=0,1,\cdots,K$$

​ 其中，$\mathbf{z}_i \sim \mathcal{N}(0,I)$。从公式可以看出，如果$\epsilon \to 0$、$K \to \infty $时，$x_K$就会近似于从$p(x)$中采样得到。

​ 这样我们就建立起了得分函数和采样之间的联系🎉

Discussion

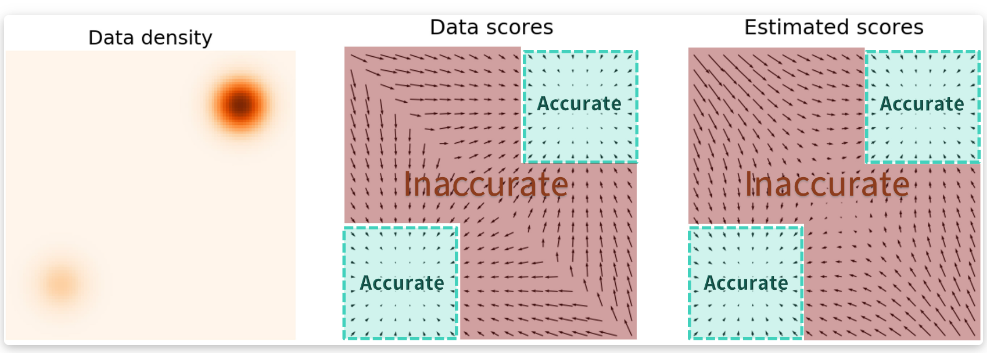
​ 基于分数的模型看似完备的过程其实也存在问题，比如在最小化期望的时候：

$$\mathbb{E}_{p(\mathbf{x})}[\lVert\nabla_{\mathbf{x}}\log p(\mathbf{x})-\mathbf{s}_{\theta}(\mathbf{x})\rVert_2^2]=\int p(\mathbf{x})\lVert\nabla_\mathbf{x}\log p({\mathbf{x}})-\mathbf{s}_\theta({\mathbf{x}})\rVert_2^2\mathrm{dx}$$

​ 相当于给$l_2$距离增加了$p(x)$这个权重，当这个权重太小时，就会导致我们在优化的过程中忽略这一部分（即所谓的低密度区域）。

​ 当数据位于高维空间时，我们的初始分布极有可能处于低密度区域，原因见这里。此时如果再有一个不准确的基于分数的模型，从一开始就将使分布偏离了正轨，使其无法产生代表数据的高质量样本。

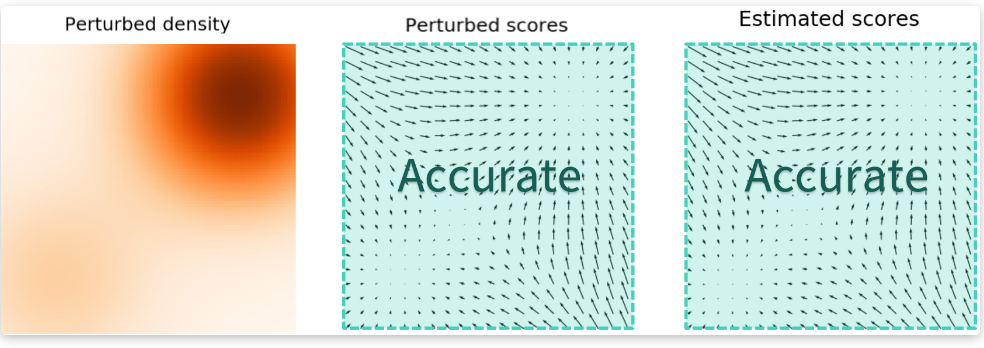
​ 类似于我们在一张HDR图片上做优化时要给亮部分和暗的部分一个平衡，不然整张图片都会被亮部决定。我们也要给原数据一些处理，让它们的分布更加“合理”，这个办法就是加高斯噪声🦄。当噪声尺度足够大时，它可以填充低数据密度区域以提高估计分数的准确性：

​ 另一个问题在于：较大的噪声可以使分布更模糊能获得更好的分数估计，但它会过度破坏原始数据；较小的噪声不能很充分覆盖低密度区域。我们还是需要一个权衡🤔。采用多个尺度的噪声扰动的方式，假设有$\sigma_1<\sigma_2<\cdots<\sigma_L$，我们的多个高斯噪声定义为$\mathcal{N}(0,\sigma_i^2I),i=1,2,\cdots,L$，对应的分布：

$$p_{\sigma_i}(\mathbf{x})=\int p(\mathbf{y})\mathcal{N}(\mathbf{x};\mathbf{y},\sigma_i^2I)\mathrm{dy}$$

​ 接下来就能计算得分函数$\nabla_\mathbf{x}\log p_{\sigma_i}(\mathbf{x})$以及对应的分数匹配，这样做其实就是模型NCSN（Noise Conditional Score-based Model）。训练的目标相应变为各个尺度的加权：

$$\sum_{i=1}^{L} \lambda(i) \mathbb{E}_{p_{\sigma_{i}}(\mathbf{x})}\left[\left\|\nabla_{\mathbf{x}} \log p_{\sigma_{i}}(\mathbf{x})-\mathbf{s}_{\theta}(\mathbf{x}, i)\right\|_{2}^{2}\right]$$

​ 权重通常设为$\lambda(i)=\sigma_i^2$。到这里，其实已经有一些DDPM的影子了😌。有了基于分数的模型的基础，我们还有另一个问题需要解决，那就是对于这种随机的过程，我们要如何表达——使用SDE来表示！

如果读过近期的扩散模型的论文，会发现其实很多时候扩散模型也被称为 Score-based Diffusion Models，以及很多关于SDE的文章（尤其是I2I任务）也会被归为扩散/分数家族🤯 。

​ 这里，我们定义SDE为：

$$d\mathbf{x}=\mathbf{f}(\mathbf{x},t)dt+g(t)d\mathbf{w}$$

​ $\mathbf{f}(*, t)$与$g(t)$分别对应漂移与扩散系数，$\mathbf{w}$为维纳过程。它的逆向过程被定义为：

$$d\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-g^2(t)\nabla_\mathbf{x}\log p_t(\mathbf{x})]dt+g(t)d \bar{\mathbf{w}}$$

​ 其中$\bar{\mathbf{w}}$为反向时间方向的维纳过程，$dt$这里是负时间的。因此，如果知道了漂移系数、扩散系数以及分布每个时间的分数，我们就能得到这个逆向的过程🥳

​ 整个过程就是（和DDPM已经非常非常像了）：

​ 我们来介绍一下主角：扩散模型🤗。

基于分数的模型还有很多可以扩展的，比如SDE的相关工作，以及本文没讲到的损失函数推导，毕竟重心并不是它们😁，在有了一点基于分数的模型直觉之后，对扩散家族能更好理解。

PS：更多内容再次推荐宋飏大佬的Blog！

Diffusion Model

Miscellaneous

​ 扩散模型与基于分数的模型类似（准确来说对图像进行噪声扰动的处理是常见的数据处理方式），我在第一次接触基于分数的模型和DDPM的时候一头雾水🫥，在不同的论文里面术语用的非常混乱，比如会把DDPM说成Score-based diffusion model的相关工作，一些22年、23年的开源的关于SDE的工作甚至也是基于Guided-diffusion框架，这让我更加一头雾水😣，不知道他们是不是一种东西。在深入了解之后，确实如宋飏博士说的：

• Collectively, these latest developments seem to indicate that both score-based generative modeling with multiple noise perturbations and diffusion probabilistic models are different perspectives of the same model family, much like how wave mechanics and matrix mechanics are equivalent formulations of quantum mechanics in the history of physics.
• Many recent works on score-based generative models or diffusion probabilistic models have been deeply influenced by knowledge from both sides of research (see a website curated by researchers at the University of Oxford). Despite this deep connection between score-based generative models and diffusion models, it is hard to come up with an umbrella term for the model family that they both belong to. Some colleagues in DeepMind propose to call them “Generative Diffusion Processes”. It remains to be seen if this will be adopted by the community in the future.

​ 也许后续会把这两种模型合二为一，互相取长补短🤔，所以我介绍了一些关于基于分数的模型的内容。

Overlook

​ 既然叫“扩散”模型，那肯定就要和物理学联系起来了😁，自然界总是朝着无序的方向发展，变得混乱，一张噪声图也可以看作是像素们逐渐“扩散”了，那有没有一种方式让这个过程可逆，找到这样的一种可逆的方式（模型），我们就能随便拿出一张“扩散了的”图像丢给模型让它给我们输出一张正常的图片。说到这，很简单的思想就是我们把每一步扩散的过程都反转过去（两极反转！），DDPM就是这样做的🤫

​ 反转噪声不是一步到位的，而是一步一步反转的，这就要求我们要把扩散的不同程度的图像都要给模型进行训练，但是我们去哪找这些图像？自己造！我们给图像添加高斯噪声，通过给定扩散程度$t$，得到$t$时刻的加了噪声的图像，给模型让它去预测噪声，这样一个过程就是DDPM的核心的两个步骤之一——前向过程。当我们训练好了这个模型，模型学习到了不同扩散程度的图片长什么样并且可以去恢复它，就可以从一张随机噪声图恢复到正常的图像😁，这就是另一个核心步骤——后向过程。

推导部分参考于原论文与Lil’Log🤗

Forward Diffusion Process➡️

前向过程

​ 正如前面所述，给定一个图片$x_0$，前向过程就是给这个图片去添加噪声，根据添加噪声的尺度（简单来说可以理解为加了几次）我们可以得到一系列的带有噪声图$\{x_1,x_2,...,x_T\}$，$T$要足够大，保证最后图像能变成一幅噪声图。很自然的，加噪的过程是一个离散时间的马尔可夫过程，因为这个过程就像是像素界的布朗运动，以美丽的光华楼为例👻：

​ 更加动态的过程：

​ 现在我们有一个先验的知识就是，图像到最后会被我们变成一个标准高斯噪声图像，那么我们就可以定义一个条件概率，以前一张图作为条件，生成下一步的图：

$$\text{q}\left(\mathbf x_t\mid\mathbf x_{t-1}\right)=\mathcal N\left(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I\right)$$

​ $\beta \in (0,1)$可以理解为步长，是一个与时间正相关的变量，随着$t$增大，$\beta$的值也增大，极端情况就是$\beta =1$时，图像就变为了纯噪声图，服从标准高斯分布。

​ 根据高斯分布的重参数化技术，$x$可重写为：

$$x=\mu(\phi)+\sigma(\phi)*\epsilon$$

​ 则条件概率重写为（把均值与方差代入）：

$$x_t=\sqrt{1-\beta_t}x_{t-1}+\sqrt{\beta_t}\epsilon_{t-1}$$

​ 这样我们就把条件概率的具体形式写出来了，并且无需考虑因为采样不可微而导致的梯度不能传播问题（可以写代码了🤣！）。但是到这还不够，刚刚说到$T$要足够大才可以，现在训练的时候$T$一般要1000~4000步，如果在训练过程中还要一步一步生成，那训练的速度也太慢了😩。好在高斯分布和马尔可夫优秀的性质，可以让我们在数学上改善这一问题。

​ 为了方便推导，现在我们假设$\epsilon \sim N(0,1)$，$\alpha_t=1-\beta_t$、$\bar{\alpha}_t=\prod_{i=1}^t\alpha_i$，推导过程（推导过程涉及了高斯分布的性质，可以详见前面部分的介绍）：

$$\begin{aligned} \mathbf{x}_{t} & =\sqrt{\alpha_{t}} \mathbf{x}_{t-1}+\sqrt{1-\alpha_{t}} \epsilon_{t-1} \\ & =\sqrt{\alpha_{t}}\left(\sqrt{\alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{1-\alpha_{t-1}} \epsilon_{t-2}\right)+\sqrt{1-\alpha_{t}} \epsilon_{t-1} \\ & =\sqrt{\alpha_{t} \alpha_{t-1}} \mathbf{x}_{t-2}+\left(\sqrt{\alpha_{t}\left(1-\alpha_{t-1}\right)} \epsilon_{t-2}+\sqrt{1-\alpha_{t}} \epsilon_{t-1}\right) \\ & =\sqrt{\alpha_{t} \alpha_{t-1}} \mathbf{x}_{t-2}+\sqrt{1-\alpha_{t} \alpha_{t-1}} \bar{\epsilon}_{t-2} \\ & =\ldots \\ & =\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \epsilon \end{aligned}$$

​ 经过推导，我们实际上得到了$q(\mathbf x_t|\mathbf x_0)=\mathcal N(\mathbf x_t;\sqrt{\bar\alpha_t}\mathbf x_0,(1-\bar\alpha_t)\mathbf I)$，在训练过程中，对于各种尺度的噪声图我们可以一步到位了。

Reverse Diffusion Process⬅️

后向过程

​ 在得到了$\{x_1,x_2,...,x_T\}$，我们就要找到一个逆向过程（同样也是马尔可夫链），当$\beta$足够小的时候，逆向过程也可以被视为是高斯的：

$$\text{q}\left(\mathbf x_{t-1}\mid\mathbf x_{t}\right)=\mathcal N\left(\mathbf x_{t-1};\sqrt{1-\beta_{t-1}}\mathbf x_{t},\beta_{t-1}\mathbf I\right)$$

​ 通过后向过程，我们就可以把一个噪声图恢复：

​ 但是我们并不能和前向过程一样，因为我们没有一个先验的知识告诉我们图像的分布是怎么样的，比如拍了一张照片，我们没法直接写出它的分布情况。除非我们把所有的图像的像素做一个统计，然后去拟合，这工作量是不可能的🫥。

​ 因此我们可以通过深度学习模型去拟合这个分布。假设我们拟合的这个分布是：

$$p_{\theta}\left(\mathbf{x}_{t-1}\mid\mathbf{x_t}\right)=\mathcal{N}\left(\mathbf{x_{t-1}}; \mu_\theta \left(\mathbf{x_t},t\right),\Sigma_\theta\left({\mathbf{x_t}},t\right)\right)$$

​ 为了得到这个分布的具体形式，作者通过一个很巧妙的裂项法，把求后向过程的概率转化成前向过程的概率的组合形式，根据贝叶斯与条件概率公式（推导中$\beta$与$\alpha$的相关定义与前向过程相同）：

$$\begin{aligned} &q\left(x_{t-1} \mid x_{t}, x_{0}\right) =q\left(x_{t} \mid x_{t-1}, x_{0}\right) \frac{q\left(x_{t-1} \mid x_{0}\right)}{q\left(x_{t} \mid x_{0}\right)} \\ & \propto \exp \left(-\frac{1}{2}\left(\frac{\left(x_{t}-\sqrt{\alpha_{t}} x_{t-1}\right)^{2}}{\beta_{t}}+\frac{\left(x_{t-1}-\sqrt{\bar{\alpha}_{t-1}} x_{0}\right)^{2}}{1-\bar{\alpha}_{t-1}}-\frac{\left(x_{t}-\sqrt{\bar{\alpha}_{t}} x_{0}\right)^{2}}{1-\bar{\alpha}_{t}}\right)\right) \\ &=\exp \\ &\left(-\frac{1}{2}(\underbrace{\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) x_{t-1}^{2}}_{x_{t-1} \text { 方差 }}-\underbrace{\left(\frac{2 \sqrt{\alpha_{t}}}{\beta_{t}} x_{t}+\frac{2 \sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} x_{0}\right) x_{t-1}}_{x_{t-1} \text { 均值 }}+\underbrace{C\left(x_{t}, x_{0}\right)}_{\text {与 } x_{t-1} \text { 无关 }})\right) \end{aligned}$$

​ 标准的高斯分布形式：

$$\exp{\left(-\dfrac{(x-\mu)^2}{2\sigma^2}\right)}=\exp\left(-\dfrac12\left(\dfrac1{\sigma^2}x^2-\dfrac{2\mu}{\sigma^2}x+\dfrac{\mu^2}{\sigma^2}\right)\right)$$

​ 二者对比可以得到：

$$\tilde{\mu}_{t}\left(x_{t}, x_{0}\right)=\frac{\sqrt{\alpha_{t}}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_{t}} x_{t}+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_{t}}{1-\bar{\alpha}_{t}} x_{0}$$

$$\frac{1}{\sigma^{2}}=\frac{1}{\tilde{\beta}_{t}}=\left(\frac{\alpha_{t}}{\beta_{t}}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)$$

​ 无关项忽略不管，这样我们就得到了方差与均值，但是均值里面还带着一个$x_0$，它在推理过程中是一个未知量，根据$x_{t}=\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}$，移向可以得到$x_0$的表达，并代入均值的表达式中，整理得到：

$$\tilde{\mu}_{t}=\frac{1}{\sqrt{\alpha_{t}}}\left(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon} \right)$$

​ 到这一步后向过程就完成了定义，首先可以发现，方差是固定不变的，只与超参数$\beta$与$\alpha$决定，因此网络要训练的就是均值这一部分。只要我们得到了均值，代入表达式就能计算得到$t-1$时刻的图像的分布是怎么样的🎉，具体而言，在均值表达式里面$x_t$是已知的，因此我们本质上是要预测$\epsilon$噪声，这（可能）也是DDPM中第一个D：Denoising的由来🤔。

Mini Summary

​ 现在我们知道了扩散模型的运作原理，现在，给定一张被噪声扰动的图像$x_t$，我们要得到$x_{t-1}$：

1. 把$x_t$送入模型，然后模型得到噪声$\epsilon$；
2. 噪声代入$\frac{1}{\sqrt{\alpha_{t}}}\left(x_{t}-\frac{\beta_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon} \right)$计算得到$x_{t-1}$的均值；
3. 根据超参数$\alpha$、$\beta$计算得到方差；
4. 把方差与均值代入重参数化后的计算式中，得到$x_{t-1}$。

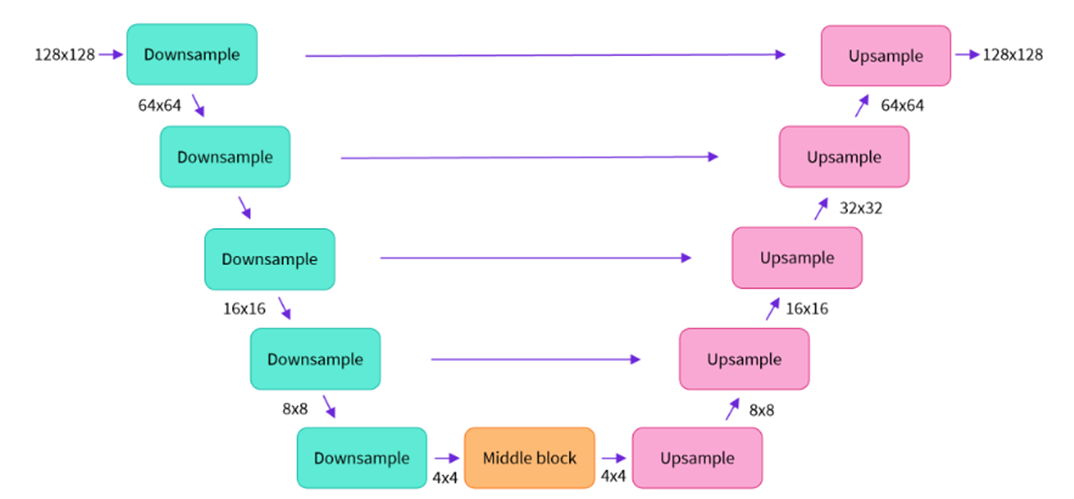
​ 所以我们选择的网络应该至少有这样的功能：输入一张图像，输出的内容应该与输入图像相同大小、通道数一致（可选）。扩散模型家族选择了U-Net网络，简要的网络结构：

​ 至此，我们还差最后一步，就是模型要怎么训练，即损失函数要如何定义🤔

Loss

​ 我们最终要用网络去拟合真实的$p_{\theta}(x_0)$，因此用最大化ELBO的方式去优化网络参数。

​ 根据后向过程我们可以发现它这个过程可以看作是一个多步、隐变量大小与图像相同的VAE，因此扩散模型的ELBO要联合所有时间$T$的损失：

$$\begin{array}{l} L=\mathbb{E}_{q\left(\mathbf{x}_{0: T)}\right.}\left[\log \frac{q\left(\mathbf{x}_{1: T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0: T}\right)}\right] \\ =\mathbb{E}_{q}\left[\log \frac{\prod_{t=1}^{T} q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{T}\right) \prod_{t=1}^{T} p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}\right] \\ =\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=1}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}\right] \\ =\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{t-1}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ =\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \left(\frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)} \cdot \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}\right)+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ =\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{0}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ =\mathbb{E}_{q}\left[-\log p_{\theta}\left(\mathbf{x}_{T}\right)+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}+\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}+\log \frac{q\left(\mathbf{x}_{1} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}\right] \\ =\mathbb{E}_{q}\left[\log \frac{q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{T}\right)}+\sum_{t=2}^{T} \log \frac{q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right)}{p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)}-\log p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)\right] \\ =\mathbb{E}_{q}[\underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{T} \mid \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{T}\right)\right)}_{L_{T}} +\sum_{t=2}^{T} \underbrace{D_{\mathrm{KL}}\left(q\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}, \mathbf{x}_{0}\right) \| p_{\theta}\left(\mathbf{x}_{t-1} \mid \mathbf{x}_{t}\right)\right)}_{L_{t-1}}-\underbrace{\log p_{\theta}\left(\mathbf{x}_{0} \mid \mathbf{x}_{1}\right)}_{L_{0}}] \\ \end{array}$$

​ $L_T$项没有可学习的参数，不需要训练，因此可以忽略；$L_0$被建模为$N(\textbf{x}_0;\boldsymbol{\mu}_\theta(\textbf{x}_1,1),\boldsymbol{\Sigma}_\theta({\textbf{x}_1},1))$；接下来就是中间$L_{t-1}$项们要怎么被参数化。

​ 由于我们是在预测噪声，因此我们可以简化中间这些项——直接计算预测的噪声与我们加入的噪声的相似度（MSE损失）：

$$\begin{array}{l} L_{t}=\mathbb{E}_{\mathbf{x}_{0}, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\mathbf{\Sigma}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|_{2}^{2}}\left\|\tilde{\boldsymbol{\mu}}_{t}\left(\mathbf{x}_{t}, \mathbf{x}_{0}\right)-\boldsymbol{\mu}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right] \\ =\mathbb{E}_{\mathbf{x}_{0,} \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_{\theta}\right\|_{2}^{2}}\left\|\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon}_{t}\right)-\frac{1}{\sqrt{\alpha_{t}}}\left(\mathbf{x}_{t}-\frac{1-\alpha_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \boldsymbol{\epsilon}_{\theta}\left(\mathbf{x}_{t}, t\right)\right)\right\|^{2}\right] \\ =\mathbb{E}_{\mathbf{x}_{0}, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_{t}\right)^{2}}{2 \alpha_{t}\left(1-\bar{\alpha}_{t}\right)\left\|\boldsymbol{\Sigma}_{\theta}\right\|_{2}^{2}}\left\|\boldsymbol{\epsilon}_{t}-\boldsymbol{\epsilon}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right] \\ =\mathbb{E}_{\mathbf{x}_{0},\epsilon}\left[\frac{\left(1-\alpha_{t}\right)^{2}}{2 \alpha_{t}\left(1-\bar{\alpha}_{t}\right)\left\|\mathbf{\Sigma}_{\theta}\right\|_{2}^{2}}\left\|\boldsymbol{\epsilon}_{t}-\boldsymbol{\epsilon}_{\theta}\left(\sqrt{\bar{\alpha}_{t}} \mathbf{x}_{0}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}_{t}, t\right)\right\|^{2}\right] \\ \end{array}$$

​ 在DDPM的论文中作者通过实验发现，把期望内的系数去掉模型会训练得更好，因此得到：

$$\begin{aligned} L_{t}^{\text {simple }} & =\mathbb{E}_{t \sim[1, T], \mathbf{x}_{0, \epsilon}, \epsilon_{t}}\left[\left\|\boldsymbol{\epsilon}_{t}-\boldsymbol{\epsilon}_{\theta}\left(\mathbf{x}_{t}, t\right)\right\|^{2}\right] \\ & =\mathbb{E}_{t \sim[1, T], \mathbf{x} 0, \epsilon_{t}}\left[\left\|\boldsymbol{\epsilon}_{t}-\boldsymbol{\epsilon}_{\theta}\left(\sqrt{\bar{\alpha}_{t} \mathbf{x}_{0}}+\sqrt{1-\bar{\alpha}_{t}} \boldsymbol{\epsilon}_{t}, t\right)\right\|^{2}\right] \end{aligned}$$

Postscript

​ 与GAN相比，扩散家族有较强的理论与数学过程，可解释性较强；并且可以生成高质量与多样的图像；最重要的是，它们在训练过程中不需要对抗过程，训练过程更稳定。

​ 另一方面，扩散模型训练过程资源消耗大；生成一张图片的采样过程耗时长；并且同样可能会受到数据集先验分布的影响，比如用狗🐕的训练集去训练不会生成猫🐱（但是比GAN能生成更多样式的狗狗）。

​ 因此从DDPM被提出以来，很多工作都基于DDPM进行了改进，并且用于不同的任务中：

• 引入条件去引导，将无条件的DDPM扩展为有条件，比如增加类别特征参与训练（Classifier-guidance），或者加入文本引导；
• 改进模型的参数，改变U-Net的网络结构使模型适合不同的任务；
• 改进采样的速度：使模型在牺牲可接受精度的前提下大大提高采样速率；
• 与基于分数的模型结合，提出很多基于SDE引导的扩散模型；
• 在图像的其他任务上广泛运用，比如分割、去噪、图像修补等；
• 引入到其他任务中，比如语音等。

​ 比较有影响力的模型包括有DDIM、SDEdit、ILVR等等，以及OpenAI提出的两个框架Improved-diffusion以及guided-diffusion，很多工作的代码都是基于这两个框架🤗，十分推荐认真研读。当然，我也有一个Toy-project来体验（生成动漫头像）。

​ 最后，本文是我研究Diffusion模型以来的一些总结，难免会有纰漏和讲得不充分的地方👻，希望能抛砖引玉。

Reference

1. Reverse Time Stochastic Differential Equations for generative modelling
2. High-Dimensional Space
3. Normal distribution - Wikipedia
4. The evidence lower bound (ELBO)
5. From Autoencoder to Beta-VAE
6. The Reparameterization Trick – Emma Benjaminson
7. Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song
8. What are Diffusion Models? | Lil’Log